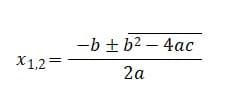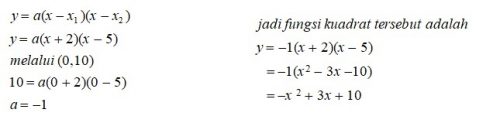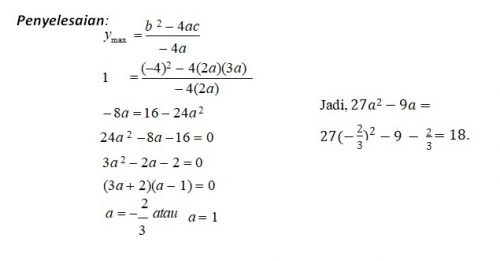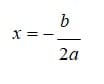Pengertian Fungsi Kuadrat
Fungsi Kuadrat – sudah tahu apa itu fungsi kuadrat? Ya, sesuai namanya, fungsi kuadrat merupakan suatu fungsi di mana pangkat tertinggi dari variabelnya adalah dua.
Fungsi Kuadrat
Fungsi Kuadrat adalah pemetaan dari daerah asal (domain) ∈ ? ke tepat satu daerah hasil (range) yang dinyatakan dengan rumus:
? = ? ? = ??2 + ?? + ?
dimana a, b, dan c adalah konstanta bilangan riil, ? ≠ 0. Dengan ?(?) atau ? disebut dengan fungsi. Bila ?1dan ?2 adalah absis titik potong pada sumbu x maka fungsi kuadrat dapat ditulis sbb:
? = ? ? = ?(? − ?1)(? − ?2)
Contoh 1:
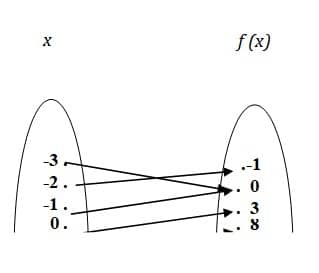
Akan ditunjukkan fungsi kuadrat ? ? = ? = ?2 + 4? + 3 bahwa untuk setiap nilai ? memetakan ke satu nilai ?.
Penyelesaian:
untuk ? = −3 → ? ? = (−3)2 + 4 −3 + 3 = 0 untuk ? = −2 → ? ? = −2 2 + 4 −2 + 3 = −1 untuk ? = −1 → ? ? = (−1)2 + 4 −1 + 3 = 0 untuk ? = 0 → ? ? = (0)2 + 4 0 + 3 = 3 untuk ? = 1 → ? ? = (1)2 + 4 1 + 3 = 8 untuk ? = 2 → ? ? = (2)2 + 4 2 + 3 = 15
Pada fungsi kuadrat ini akan diselidiki mengenai:
- Pembuat nol ?(?) atau harga nol ?(?).
- Nilai-nilai ekstrim dari ?(?).
- Pembuat nol dari ? ? = ??2 + ?? + ?
Maksud pembuat nol disini adalah nilai ? yang menyebabkan ? ? = 0. Untuk mencari nilai ? dapat menggunakan rumus persamaan kuadrat sebagai berikut:
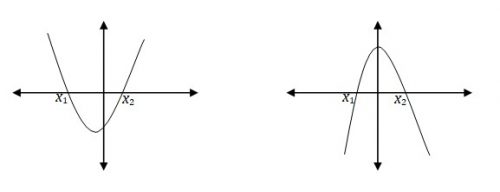
- Jika ? > 0, maka akan didapat dua nilai pembuat nol yaitu ?1dan ?2, ?1 ≠ ?2.
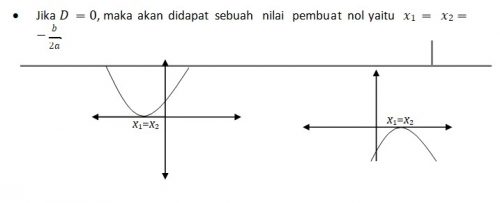
- Jika ? < 0, maka tidak ada nilai pembuat
Fungsi seperti ini (D < 0) mempunyai 2 harga definit yaitu :
- Definit Positif
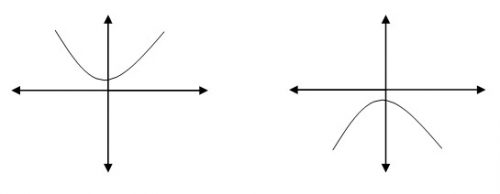
Fungsi akan selalu berharga positif untuk setiap harga x atau grafik fungsi seluruhnya berada diatas sumbu x. Syaratnya a > 0, D < 0
- Definit Negatif
Fungsi akan selalu berharga negatif untuk setiap harga x atau grafik fungsi seluruhnya berada dibawah sumbu x. Syaratnya a < 0, D < 0
- Nilai Ekstrim
Nilai Ekstrim ada dua kategori yaitu ekstrim maksimum (???? ) dan ekstrim minimum (???? ).
? = ? ? = ??2 + ?? + ?
Dapat diubah menjadi:
Contoh 1:
Jika ? ? = ?2 − ?? + 7 puncaknya berabsis 4, maka ordinatnya adalah…
Contoh 2:
Tentukan fungsi kuadrat yang melalui titik potong pada sumbu x yaitu -2 dan 5, serta memotong sumbu y pada (0,10).
Penyelesaian:
Titik potong pada sumbu x: (-2,0) dan (5,0) dan titik potong pada sumbu y: (0,10)
Fungsi kuadratnya yaitu:
Contoh 3:
Nilai tertinggi fungsi ? ? = ??2 + 4? + ? ialah 3, sumbu simetrinya adalah…
Penyelesaian:
Karena titik puncaknya adalah maksimum, maka pilih ? < 0, yaitu a = -1. Sehingga sumbu simetrinya adalah:
Contoh 4:
Jika fungsi kuadrat ? ? = 2??2 − 4? + 3? mempunya nilai maksimum 1, maka 27?2 − 9? = ⋯
Contoh 5:
Fungsi kuadrat yang grafiknya melalui titik (-1,3) dan titik terendahnya sama dengan puncak grafik ? ? = ?2 + 4? + 3 adalah…
Contoh 6:
Tentukan a agar fungsi f(x) = x2 +4x + (a – 3) harganya selalu positif untuk setiap harga x ?
Penyelesaian :
Definit positif → syaratnya ? > 0 sudah dipenuhi
D < 0 → 16 – 4 (1) (a – 3) < 0
16 – 4a + 12 < 0
-4a < 0
a > 7
- Grafik Fungsi Kuadrat
Himpunan titik-titik (x,y) yang memenuhi ? = ?(?) = ??2 + ?? + ?, a → 0 adalah parabola. Sedangkan ? = ?(?) = ??2 + ?? + ? disebut persamaan parabola.
Untuk melukis grafik fungsi :
? = ?(?) = ??2 + ?? + ?
Diperlukan syarat-syarat sebagai berikut :
- Titik potong dengan sumbu x
Syarat f(x) = 0 → ax2 + bx + c = 0
(x – x1) (x – x2) → (x1, 0) dan (x2, 0)
- Titik potong dengan sumbu y
Syarat x = 0 → f(0) = a(0)2 + b (0) + c
f(x) = c → (0,c)
- Sumbu Simetri
- Titik balik / Titik puncak
Titik balik atau titik puncak adalah:
Parabola mencapai titik balik minimum jika a >0 dan parabola mencapai titik balik maksimum jika a <0.
Contoh 7:
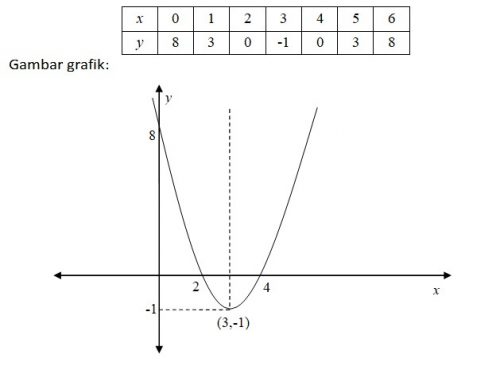
Gambarlah grafik fungsi: f (x) → x2 → 6x → 8
Penyelesaian:
Jadi puncaknya adalah p (x,y) → p (3,-1). Untuk mendapatkan gambar grafik yang baik kita menggunakan tabel fungsi sebagai berikut:
Demikian sedikit pembahasan mengenai Fungsi Kuadrat semoga dengan adanya pembahasan ini dapat menambah wawasan dan pengetahuan untuk kita semua, dan kami ucapkan Terima Kasih telah menyimak ulasan kami. Jika kalian merasa ulasan kami bermanfaat mohon untuk dishare 🙂
Baca juga artikel lainnya tentang: