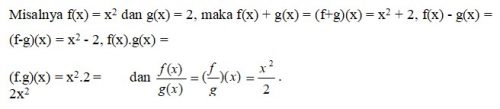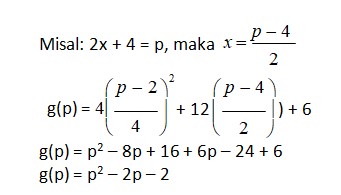Fungsi Komposisi

Fungsi Komposisi – Fungsi Komposisi adalah penggabungan sebuah operasi dua jenis fungsi f(x) dan g(x) sehingga dapat menghasilkan sebuah fungsi baru. Tinjau fungsi-fungsi dengan domain dan kodomainnya berupa himpunan bagian dari bilangan real. Ada beberapa nama fungsi seperti fungsi konstan linear, kuadrat atau fungsi polinom, fungsi nilai mutlak, fungsi trigonometri, fungsi logaritma, fungsi eksponen dan lain sebagainya. Bila kita memiliki sebuah himpunan fungsi, maka kita dapat melakukan operasi penjumlahan, pengurangan, perkalian dan pembagian pada fungsi-fungsi itu.

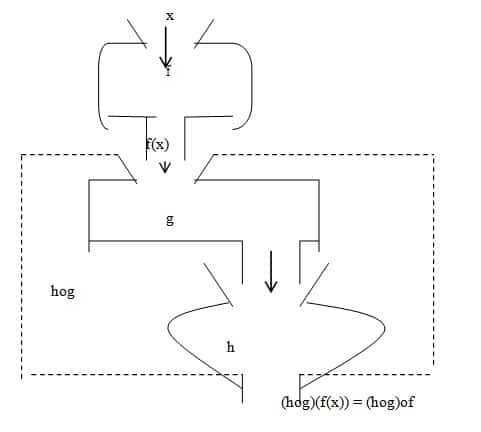
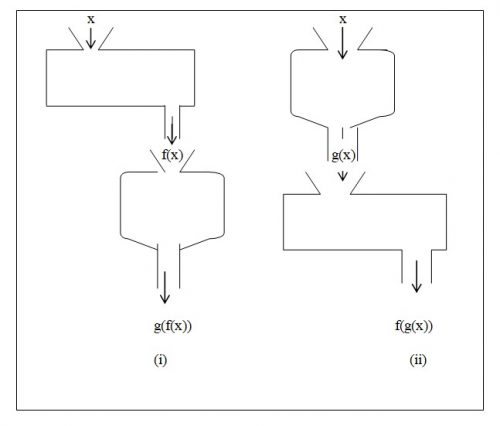
Sekarang perhatikan apabila kita memiliki dua mesin fungsi f dan g bekerja secara berurutan, f dilanjutkan dengan g atau g dilanjutkan dengan f, seperti terlihat pada Gambar dibawah ini.

Misalkan f dan g berturut-turut memiliki aturan f(x) = x², g(x) = x-1.

Sifat-sifat Komposisi Fungsi

Apa yang dimaksud operasi hitung pada himpunan bilangan ? Penjumlahan, pengurangan, perkalian, pembagian, pengkuadratan, penarikan akar pangkat dua merupakan contoh-contoh operasi hitung. Penjumlahan, pengurangan, perkalian, dan pembagian termasuk pada operasi biner.

Sedangkan pengkuadratan dan penarikan akar pangkat dua termasuk pada operasi uner. Jika operasi itu dipandang sebagai mesin produksi, operasi biner merupakan mesin yang memiliki dua masukan (input) dan sebuah keluaran (output). Sedangkan operasi uner suatu mesin yang memiliki sebuah input dan sebuah output.

Komposisi fungsi dapat dipandang sebagai operasi biner, dengan memiliki input dua buah fungsi dan ouputnya sebuah fungsi. Komposisi fungsi memiliki sifat-sifat sebagai berikut.

Pada umumnya gof fog, ini menyimpulkan bahwa komposisi fungsi tidak memenuhi sifat komutatif.
Asosiatif, yaitu bila f, g dan h fungsi maka (fog)oh = fo(goh).

Misalkan f , g, dan h fungsi, bahwa komposisi fungsi bersifat sifat asosiatif yaitu, fo(goh) = (fog)oh.

Sebagai contoh

Misalkan f(x) = 2x +3, g(x) = x2 dan h(x) = 2 –x Carilah fo(goh) dan (fog)oh

Jawab

(goh)(x) = g(h(x)) = g(2 –x) = (2-x)2 = 4 – 4x + x2.

fo(goh) = (fo(goh))(x) = f((goh))(x) = f(4 – 4x + x2) = 2(4 – 4x + x2) + 3

= 8 -8x + 2×2 + 3 = 11 – 8x + 2×2 = 2×2 -8x + 11

(fog)(x) = f(g(x)) = f(x2) = 2(x2) + 3 = 2×2 + 3

((fog)oh) = ((fog)oh))(x) = (fog)((2-x) = 2(2-x)2 + 3 = 2(4 -4x + x2) + 3

= 8 -8x + 2×2 + 3 = 11 – 8x + 2×2. = 2×2 -8x + 11.

Memiliki unsur identitas, yaitu I(x) = x, sehingga untuk setiap fungsi f berlaku foI = Iof = f. Sebagai contoh, bila f(x) = x2 -3x, maka (foI)(x) = f(I(x)) = f(x) = x2 -3x, juga (Iof)(x) = I(f(x)) = x2 -3x = f(x).
Bila f korespondensi satu-satu, maka ada fungsi invers dengan lambang f-1 sehingga fof-1 = f-1of = I. Sebagai contoh, bila f(x) = x -3 maka f-1(x) = x + 3 sebab (fof-1)(x) = (x+3) – 3 = x = I(x) dan (f-1of)(x) = (x-3) + 3 = x = I(x).

Contoh Soal Fungsi Komposisi

Perhatikan contoh berikut:

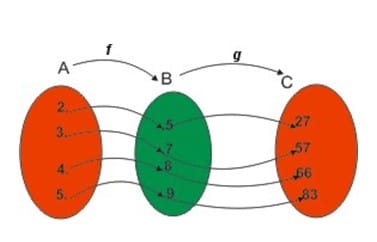
Ada 3 himpunan yaitu, A = {2, 3, 4, 5}, B = {5, 7, 9, 11} dan C = {27, 51, 66, 83}.

f: A→ B ditentukan dengan rumus f (x) → 2x → 1 dengan g : B → C ditentukan oleh

rumus

g(x) → x2 → 2 . Ditunjukkan oleh diagram panah sbb:

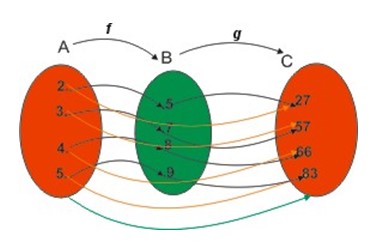
Jika h fungsi dari A ke C sehinnga: peta dari 2 adalah 27

peta dari 3 adalah 51

peta dari 4 adalah 66

peta dari 5 adalah 83

dan diagaram panahnya menjadi,

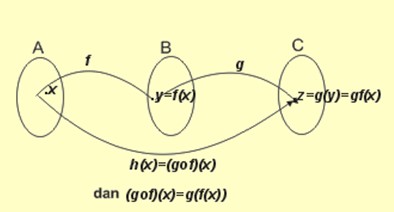
fungsi dari h dari A ke C disebut fungsi komposisi dari g dan f ditulis h = g o f atau h(x) = (g o f )(x).

Secara umum:

Definisinya begini:

Misalkan fungsi

f : A → B ditentukan dengan rumus y = f (x)

g : B → C ditentukan dengan rumus y = g(x)

Fungsi komposisi g dan f ditentukan dengan autan:

h(x) = (g = f )(x) = g( f (x))

o dibaca komposisi atau “bundaran”

Perhatikan bahwa dalam fungsi komposisi (g o f )(x) = g( f (x)) ditentukan dengan f (x) terlebih dahulu kemudian dilanjutkan dengan pengerjaan oleh pengerjaan g(x).

Perhatikan contoh berikut:

Contoh:

Diketahui f(x) = x2 + 1 dan g(x) = 2x – 3.

Tentukan:

(f o g)(x)
(g o f)(x)

Jawab:

1. (f o g)(x) = f (g(x))

= f(2x – 3)

= (2x – 3)2 + 1

= 4×2 – 12x + 9 + 1

= 4×2 – 12x + 10

2. (g o f)(x) = g (f(x))

= g(x2 + 1)

= 2(x2 + 1) – 3

= 2×2 – 1

Ternyata, ( f o g)(x) ≠ (g o f )(x). Jadi pada komposisi fungsi tidak berlaku sifat komutatif.

Diketahui f : R → R dan g : R → R ditentukan oleh f(x) = x + 3 dan (f o g)(x) = x2 + 6x + 7, maka tentukan g(x) !

Jawab :

f(x) = x + 3

(f o g)(x) = x2 + 6x + 7 f(g(x)) = x2 + 6x + 7 g(x) + 3 = x2 + 6x + 7

g(x) = x2 + 6x + 4

Diketahui f : R  R dan g : R  R ditentukan oleh f(x) = 2x + 4 dan (g o f)(x) = 4×2 + 12x + 6, maka tentukan g(x).

Jawab :

(g o f)(x) = 4×2 + 12x + 6

g(f(x)) = 4×2 + 12x + 6

g(2x + 4) = 4×2 + 12x + 6

Cara lain:

(g o f )(x) = g( f (x)) = g(2x + 4) = 4x2 + 12x + 6

(2x + 4)2 – 2(2x + 4) – 2

Jadi,

g(x) = x2 – 2x – 2

Demikian sedikit pembahasan mengenai Fungsi Komposisi semoga dengan adanya pembahasan ini dapat menambah wawasan dan pengetahuan untuk kita semua, dan kami ucapkan Terima Kasih telah menyimak ulasan kami. Jika kalian merasa ulasan kami bermanfaat mohon untuk dishare 🙂