Mengenal Fungsi Eksponen Beserta Contohnya

Fungsi.co.id – Mengenal Fungsi Eksponen Beserta Contohnya – Eksponen atau lebih sering kita mendengar nama pangkat adalah nilai yang menunjukkan tingkat peringkat atau sebanyak yang dikalikan dengan angka.

Jika ada dua angka dan B, maka notasi dari eksponen matematika adalah AB yang kemudian membaca peringkat b.

Angka yang kemudian disebut sebagai angka dasar (kepala sekolah) dan b disebut eksponen.

Jika B adalah integer positif, eksponen dapat dinyatakan

ab = a x a x a x … x a (sejumlah faktor b). Namun Anda tahu apa fungsi eksponen? Selanjutnya kita akan menjelaskan detail lebih lanjut tentang eksponen, jangan ingin tahu mari kita baca artikel di bawah ini dengan cermat.

Daftar Isi

1 Mengenal Fungsi Eksponen Beserta Contohnya
- 1.1 Fungsi Eksponen Memiliki Sifat Termasuk
2 Persamaan Fungsi Eksponen
3 Pertidaksamaan Fungsi Eksponen
4 Contoh Fungsi Eksponen

Mengenal Fungsi Eksponen Beserta Contohnya

Jika ada bilangan real x, maka fungsi eksponen adalah fungsi yang memetakan nomor X ke AX dengan kondisi A> 0 dan A ≠ 1 atau dapat ditulis F: (x) = AX.

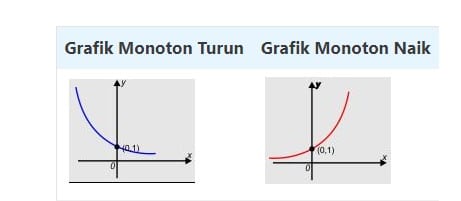
Untuk grafik itu

Fungsi Eksponen Memiliki Sifat Termasuk

Kurva berada di atas sumbu x (pasti pasti)
Potong sumbu y pada (0,1)
Memiliki ASIMTO Y = 0 (SB. X)
Untuk x> 1, maka grafik monoton naik
Untuk 0 <x <1, maka grafik monoton turun

Persamaan Fungsi Eksponen

Seperti fungsi fungsi lainnya, dalam bahan fungsi eksponen juga ada persamaan fungsi eksponen.

Nah, untuk A> 0 dan a ≠ 1, beberapa bentuk persamaan fungsi eksponen dan solusinya adalah

Jika AF (x) = dan kemudian f (x) = n

Jika AG (x) = Ah (x) lalu g (x) = h (x)

Jika AF (x) = bf (x) maka f (x) = 0

Jika f (x) g (x) = f (x) h (x) maka kemungkinan penyelesaian adalah

g (x) = h (x)

f (x) = 1

f (x) = -1 jika g (x) dan h (x) sama-sama ganjil atau bahkan

f (x) = 0 jika g (x)> 0 dan h (x) <0

Jika f (x) h (x) = g (x) h (x) maka kemungkinan penyelesaian adalah

f (x) = g (x)

h (x) = 0 jika g (x) dan h (x) tidak sama dengan 0

Jika f (x) g (x) = 1 maka kemungkinan penyelesaian adalah

f (x) = 1

g (x) = 0 jika f (x) ≠ 0

f (x) = -1 jika g (x) Genap

Pertidaksamaan Fungsi Eksponen

Jika ada persamaan fungsi eksponya, ada juga kesetaraan fungsi eksponen. Penyelesaian persamaan fungsi eksponen adalah sebagai berikut

Untuk A> 1

Jika AF (x) <AG (x) maka f (x) <g (x)

Jika AF (x)> AG (x) maka f (x)> g (x)

untuk 0 <A <1

Jika AF (x) <AG (x) maka f (x)> g (x)

Jika AF (x)> AG (x) maka f (x) <g (x)

Contoh Fungsi Eksponen

x5 = x (3 + 5) = x8
(x3.y2) 2 = x3.2. Y2.2 = x6.y4.
Jika f (x) = 3x + 2 Cari nilai F (3) dan F (-3)
f (3) = 33 + 2 = 35 = 243
f (-3) = 3-3 + 2 = 3-1 = 1/3 = 0,333

Temukan Nilai X Yang Memenuhi 3x-3 = 0

3x-3 = 0

3x = 31.

x = 1 maka x yang Anda cari adalah x = 1

Tentukan Nilai X Yang Memenuhi Persamaan Eksponen 4x + 2 + 4x = 17!

Diskusi

4x + 2 + 4x = 17

4x.42 + 4x = 17

16.4x + 4x = 17

17.4x = 17.

4x = 1.

x = 0.

Jadi, nilai X yang memenuhi persamaan eksponen 4x + 2 + 4x = 17 adalah 0.

Persamaan Akar 253x-6 = 54x ^ 2-12x + 2 Adalah P Dan Q. Apa Nilai PQ?

Diskusi

253x-6 = 54x ^ 2-12x + 2

52 (3x-6) = 54x ^ 2-12x + 2

2 (3x-6) = 4×2 – 12x + 2

6x – 12 = 4×2 – 12x + 2

4×2 – 12x + 2 – 6x + 12 = 0

4×2 – 18x +14 = 0

pq = c / a = 14/4 = 3.5

Jadi, nilai PQ adalah 3.5.

Dikenal 32x – 1 – 1 = 2.3x-1. Hitung Nilai 9x!

Diskusi

32x – 1 – 1 = 2.3x-1

32x / 31 – 1 = 2.3x / 31

32x – 3 = 2.3x

32x -2.3x – 3 = 0

Misalnya a = 3x, kalau begitu

32x – 2.3x – 3 = 0

A2 – 2A – 3 = 0

(A-3) (A + 1) = 0

A = 3 atau A = -1

Karena, a = -1 mungkin tidak memenuhi A = 3x, lalu a = 3.

Yang seperti itu

A = 3x.

3 = 3x.

31 = 3x.

x = 1.

9x = 91 = 9

Jadi, nilai 9x adalah 9.

Jika 3x – Y = 81 Dan 2x – 2y = 1/16, Tentukan Nilai X + Y!

Diskusi

3x – y = 81

3x – y = 34

x – y = 4

x = y + 4 … (1)

2x – 2y = 1/16

2x – 2y = 2-4

X – 2y = -4 … (2)

Substitusi (1) hingga (2), sehingga diperoleh

X – 2y = 4

Y + 4 – 2Y = -4

-Y = -8.

Y = 8.

Substitusi nilai y ke (1), jadi diperoleh

x = y + 4

x = 8 + 4

x = 12.

x + y = 8 + 12 = 20

Jadi, nilai X + Y adalah 20.

Tentukan Nilai 31 / N Jika Diketahui (90.125) N = √3.

Diskusi

(90.125) n = √3

90.125N = √3.

32 (0.125) n = 3½

30.25n = 3½.

0,25N = ½.

n = 2.

Jadi diperoleh

31 / n = 3½ = √3

Jadi, nilai 31 / n adalah √3.

Demikian sedikit pembahasan mengenai Mengenal Fungsi Eksponen Beserta Contohnya semoga dengan adanya pembahasan ini dapat menambah wawasan dan pengetahuan untuk kita semua, dan kami ucapkan Terima Kasih telah menyimak ulasan kami. Jika kalian merasa ulasan kami bermanfaat mohon untuk dishare :).